Periodo de semidesintegración radiactiva
La desintegración radiactiva se comporta en función de la ley de decaimiento exponencial:
N(t) = N0e − λt,
donde:
- N(t) es el número de radionuclidos existentes en un instante de tiempo t.
- N0 es el número de radionúclidos existentes en el instante inicial t = 0.
- λ, llamada constante de desintegración radiactiva, es la probabilidad de desintegración por unidad de tiempo. A partir de la definición de actividad, es evidente que la constante de desintegración es el cociente entre el número de desintegraciones por segundo y el número de átomos radiactivos (
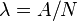 ).
).
Se llama tiempo de vida o tiempo de vida media de un radioisótopo el tiempo promedio de vida de un átomo radiactivo antes de desintegrarse. Es igual a la inversa de la constante de desintegración radiactiva ( ).
).
 ).
).Al tiempo que transcurre hasta que la cantidad de núcleos radiactivos de un isótopo radiactivo se reduzca a la mitad de la cantidad inicial se le conoce como periodo de semidesintegración, período, semiperiodo, semivida o vida media (no confundir con el ya mencionado tiempo de vida) (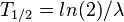 ). Al final de cada período, la radiactividad se reduce a la mitad de la radiactividad inicial. Cada radioisótopo tiene un semiperiodo característico, en general diferente del de otros isótopos.
). Al final de cada período, la radiactividad se reduce a la mitad de la radiactividad inicial. Cada radioisótopo tiene un semiperiodo característico, en general diferente del de otros isótopos.
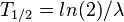 ). Al final de cada período, la radiactividad se reduce a la mitad de la radiactividad inicial. Cada radioisótopo tiene un semiperiodo característico, en general diferente del de otros isótopos.
). Al final de cada período, la radiactividad se reduce a la mitad de la radiactividad inicial. Cada radioisótopo tiene un semiperiodo característico, en general diferente del de otros isótopos.Ejemplos:
| Isótopo | Periodo | Emisión |
|---|---|---|
| Uranio-238 | 4510 millones de años | Alfa |
| Carbono-14 | 5730 años | Beta |
| Cobalto-60 | 5,271 años | Gamma |
| Radón-222 | 3,82 días |
| Alfa |
La velocidad de desintegración es la tasa de variación del número de núcleos radiactivos por unidad de tiempo:
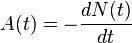
Dada la ley de desintegración radiactiva que sigue N(t) (ver Periódo de semidesintegración), es evidente que:
 ,
,donde:
 es la actividad radiactiva en el instante
es la actividad radiactiva en el instante  .
.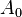 es la actividad radiactiva inicial (cuando
es la actividad radiactiva inicial (cuando  ).
). es la base de los logaritmos neperianos.
es la base de los logaritmos neperianos. es el tiempo transcurrido.
es el tiempo transcurrido. es la constante de desintegración radiactiva propia de cada radioisótopo.
es la constante de desintegración radiactiva propia de cada radioisótopo.
La actividad también puede expresarse en términos del número de núcleos a partir de su propia definición. En efecto:
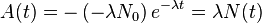
No hay comentarios:
Publicar un comentario